使用python实现归并排序算法
# 归并排序简介
归并排序 ——
MERGE-SORT,归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。 归并排序适用于子序列有序的数据排序
# 思路
归并排序是分治法的典型应用。分治法(Divide-and-Conquer):将原问题划分成 n 个规模较小而结构与原问题相似的子问题;递归地解决这些问题,然后再合并其结果,就得到原问题的解
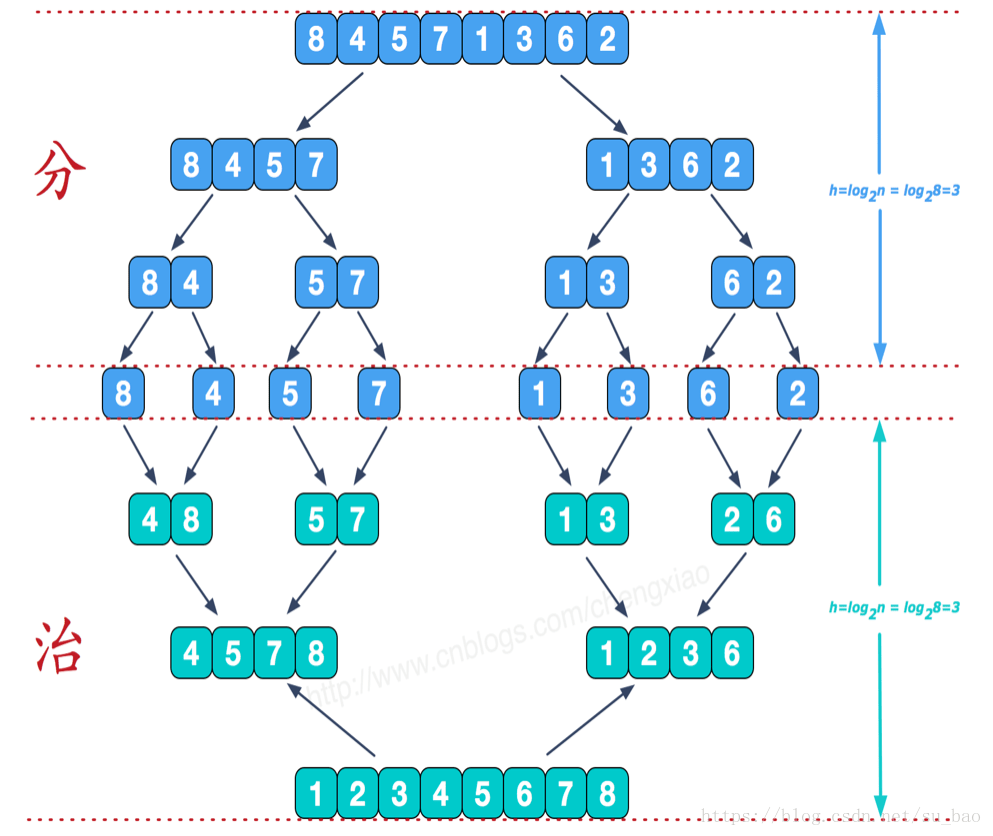
从上图看分解后的数列很像一个二叉树
归并排序采用分而治之的原理:
- 将一个序列从中间位置分成两个序列
- 在将这两个子序列按照第一步继续二分下去
- 直到所有子序列的长度都为1,也就是不可以再二分截止。这时候再两两合并成一个有序序列即可
# 举例
# 1. 对以下数组进行归并排序:
[11, 99, 33 , 69, 77, 88, 55, 11, 33, 36,39, 66, 44, 22]
# 2. 首先,进行数组分组,即
[11, 99, 33 , 69, 77, 88, 55] [ 11, 33, 36,39, 66, 44, 22]
[11, 99, 33] [69, 77, 88, 55] [ 11, 33, 36] [39, 66, 44, 22]
[11] [99, 33] [69, 77] [88, 55] [11] [33, 36] [39, 66] [44, 22]
# 直到所有子序列的长度都为1,也就是不可以再二分截止。
[11], [99], [33] , [69], [77], [88], [55],[ 11], [33], [36],[39], [66], [44], [22]
# 3. 这时候再两两合并成一个有序序列即可。
[11],[33,99],[69,77],[55,88],[11],[33,36],[39,66],[22,44]
[11,33,99],[55,69,77,88],[11,33,36],[22,39,44,66]
[11,33,55,69,77,88,99],[11,22,33,36,39,44,66]
# 4、最终排序
[11, 11, 22, 33, 33, 36, 39, 44, 55, 66, 69, 77, 88, 99]
# 递归版本
递归版本相对比较好理解
import random
def marge(left, right):
"""排序合并两个数列"""
result = []
# 两个数列都有值
while len(left) > 0 and len(right) > 0:
# 左右两个数列第一个最小放前面
if left[0] <= right[0]:
result.append(left.pop(0))
else:
result.append(right.pop(0))
# 只有一个数列中还有值,直接添加
result += left
result += right
return result
def merge_sort(arr):
"""归并排序"""
if len(arr) == 1:
return arr
# 使用二分法将数列分两个
mid = len(arr) // 2
left = arr[:mid]
right = arr[mid:]
# 使用递归运算
return marge(merge_sort(left), merge_sort(right))
arr_s = [random.randint(0, 100) for _ in range(10)]
print(arr_s)
restult = merge_sort(arr_s)
print(restult)
结果:
# source:
[68, 67, 4, 0, 49, 98, 56, 39, 59, 22]
# result
[0, 4, 22, 39, 49, 56, 59, 67, 68, 98]
# 非递归版本
非递归版本从 分 的最后一步开始,往上归并
PS: 非递归版本运行的时间空间效率均高于递归版本,不需要额外的空间。直接在原数组上进行切割合并
import random
def merge_2(seq, low, mid, high):
left = seq[low: mid]
right = seq[mid: high]
k = 0
j = 0
result = []
while k < len(left) and j < len(right):
if left[k] <= right[j]:
result.append(left[k])
k += 1
else:
result.append(right[j])
j += 1
result += left[k:]
result += right[j:]
seq[low: high] = result
def merge_sort_2(seq):
i = 1 # i是步长
while i < len(seq):
low = 0
while low < len(seq):
mid = low + i # mid前后均为有序
high = min(low + 2 * i, len(seq))
if mid < high:
merge_2(seq, low, mid, high)
low += 2 * i
i *= 2
arr = [random.randint(0, 100) for _ in range(10)]
print("\n\n" + f"{arr}")
merge_sort_2(arr)
print(arr)
# 结尾
比较性: 排序时元素之间需要比较,所以为比较排序
稳定性: 我们从代码中可以看到当左边的元素小于等于右边的元素就把左边的排前面,而原本左边的就是在前面,所以相同元素的相对顺序不变,故为稳定排序
时间复杂度: 复杂度为O(nlog^n)
空间复杂度: 在合并子列时需要申请临时空间,而且空间大小随数列的大小而变化,所以空间复杂度为O(n)
记忆方法:所谓归并肯定是要先分解,再合并
# 额外话题
python中有归并排序的算法库 heapq,使用方式如下,有关heapq 库会在后面专门提到
from heapq import merge
def merge_sort(seq):
if len(seq) <= 1:
return seq
else:
middle = len(seq) // 2
left = merge_sort(seq[:middle])
right = merge_sort(seq[middle:])
return list(merge(left, right)) #heapq.merge()
if __name__=="__main__":
seq = [1,3,6,2,4]
print(merge_sort(seq))
TIP
heapq.merge 可迭代特性意味着它不会立马读取所有序列。 这就意味着你可以在非常长的序列中使用它,而不会有太大的开销比如,下面是一个例子来演示如何合并两个排序文件:
import heapq
with open('sorted_file_1', 'rt') as file1, open('sorted_file_2', 'rt') as file2, open('merged_file', 'wt') as outf:
for line in heapq.merge(file1, file2):
outf.write(line)
# 或者直接合并两个排序好的数组
a = [1, 4, 7, 10]
b = [2, 5, 6, 11]
print(list(heapq.merge(a, b)))
WARNING
heapq.merge() 需要所有输入序列必须是排过序的。特别的,它并不会预先读取所有数据到堆栈中或者预先排序,也不会对输入做任何的排序检测。
它仅仅是检查所有序列的开始部分并返回最小的那个,这个过程一直会持续直到所有输入序列中的元素都被遍历完。